আমাদের জিবনে সমকোণী ত্রিভুজের ব্যবহার অনেক। আমাদের পরিবেশে কল্পনায় হাজারো সমকোণী ত্রিভুজ গঠন করা যেতে পারে। এই সমকোণী ত্রিভুজ ব্যবহার করে, আমরা গাছে না উঠেও সহজে বের করতে পারি গাছের উচ্চতা, বের করতে পারি নদীর প্রস্থ থেকে শুরু করে দূরবর্তী গ্রহ নক্ষত্রের দূরত্ব। আর এই গাণিতিক কৌশলের ভিত্তিতেই সৃষ্টি হয়েছিল ত্রিকোনমিতি নামক গণিতের বিশেষ শাখা। এটি মূলত ৩ কোণের পরিমাপের বিষয় নিয়েই সৃষ্টি।
আমরা সকলেই জানি যে, যেকোন কোণের (সমকোণ ব্যাতিত) ছয়টি ত্রিকোণমিতিক অনুপাত পাওয়া যায়। যথাঃ sin@,cos@,tan@,cosec@,sec@ ও cot@.
আমরা পাঠ্যাবইয়ের বিভিন্ন সমস্যার সমাধান করবার জন্য সাধারনত (০,৩০,৪৫,৬০,৯০) এই ৫ টি কোণের জন্য বাহুদ্বয়ের অনুপাত বের করি এবং এগুলো দিয়েই বিভিন্ন বাস্তবিক সমস্যার সমাধান করি। তবে সমস্যা হলো ৬ টি ত্রিকোনমিতিক অনুপাতের ৫ টি কোণের জন্য অনুপাতসমূহ(৩০ টি) মুখস্থ করতে অনেকেরই সমস্যা হয়। অনেক ছাত্রছাত্রী তো মুখস্থ না করেই ক্যালকুলেটর বা বইয়ের সাহায্য নিয়ে পড়াশোনা শেষ করে দিতে চাই। অনেকেই আবার মুখস্থ করেও ভুলে যায়। অনেকের ভালোভাবে মুখস্থ থাকলেও পরীক্ষার সময়ে সন্দেহ সৃষ্টি হয় বা গুলিয়ে দিয়ে ভুল করে দেয়।
তাই খুব সহজেই ত্রিকোণমিতিক এই অনুপাতগুলো মনে রাখার কৌশল খুবই জরুরী।
চলুন এবার তবে সেই কৌশল শিখা যাক যে কি করে সহজেই খুবই অল্প সময়ে এই অনুপাতগুলো বের করা যায়।
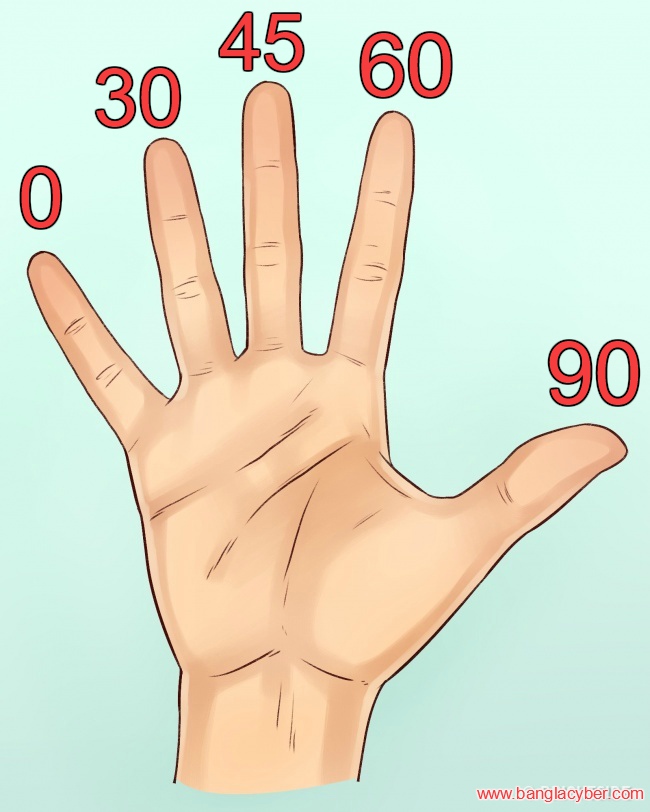
আপনারা সকলেই নিশ্চয়ই চিত্রে একটি হাতের ছবি দেখতে পাচ্ছেন।
এবার হাত এর ছবিতে লক্ষ্য করেছেন নিশ্চয়ই যে ৫ টি আঙুলকে (০,৩০,৪৫,৬০,৯০) কোণের চিহ্ন হিসেবে ধরা হয়েছে। এবার চলুন নিজ নিজ হাত দিয়ে অনুপাতগুলো বের করি।
প্রথমে sin এর ৫টি কোণের অনুপাত বের করি চলুন।
নিজ নিজ হাতের আঙুলগুলোকে চিত্রের হাতের মতো করে ভাবুন। এই sin এর অনুপাতগুলো বের করার জন্য যে কোণের মান বের করবেন সেই কোণ অনুযায়ী চিত্রের ছবির মতো আঙুল সিলেক্ট করুন। তারপর দেখুন যে ঐ আঙুলের বাম পাশে কতটি আঙুল আছে। বামপাশে যতগুলে আঙুল থাকবে, তার বর্গমূল করে ২ দিয়ে ভাগ করলেই, ঐ কোণের মান পেয়ে যাব আমরা।
উদাহরণঃ এবার sin0 ডিগ্রী এর মানের জন্য আমরা ভাবি। চিত্রের হাতের ০ লেখা জায়গার বামপাশে কি আর কোন আঙুল আছে..?
না,নেই। (সুতরাং, ০ টি আঙুল আছে)
তার মানে ০ কে বর্গমূল করে ২ দিয়ে ভাগ করলেই sin0 এর মান পাওয়া যাবে।
সুতরাং,sin0= √ 0/2 =0
অনুরুপভাবে,sin30= √ 1/2 =1/2
sin45= √ 2/2 = √2/ √2* √2 =1/ √2
sin60 = √3/2
sin90= √4/2=2/2=1
sin এর অনুপাতগুলো পেয়ে যাবার মানে cosec এর অনুপাতগুলোও পেয়ে গেছি।
কারন, sin@=1/cosec@
তাই,cosec0=1/0=অনির্ণেয়
cosec30=2….(এভাবে বের করতে হবে)
আমরা sin এর অনুপাতগুলো বের করতে শিখলাম। এবার আমরা cos এর অনুপাতগুলো বের করতে শিখব।
cos এর কোণের অনুপাতসমূহ বের করার পদ্ধতি sin এর মতোই,শুধুমাত্র একটু উল্টা।
cos এর ক্ষেত্রেও আমার ছবির মতো আঙুল সিলেক্ট করতে হবে। এরপর যে কোণের মান বের করব সেই কেণ সিলেক্ট করা আঙুলের ডানপাশের আঙুল সংখ্যা হিসেব করে বর্গমূল করার পরে ২ দিয়ে ভাগ করলেই,উক্ত কোণের মান পাওয়া যাবে।
উদাহরণঃ এবার cos0 ডিগ্রী এর মানের জন্য আমরা ভাবি। চিত্রের হাতের ০ লেখা জায়গার ডানপাশে কি আর কোন আঙুল আছে..?
৪ টি আঙুল আছে
তার মানে ৪ কে বর্গমূল করে ২ দিয়ে ভাগ করলেই cos0 এর মান পাওয়া যাবে।
cos0= √4/2 =2/2 =1
cos30= √3/2
cos45 = √2/2= √2/ √2. √2=1/ √2
cos60 = √1/2 =1/2
cos90=0/2 =0
এবার cos থেকে আমরা সহজেই sec এর কোণের অনুপাতগুলো বের করতে পারি।
কারণ,cos@=1/sec@
অর্থ্যাৎ,sec=1
sec30=2/ √3(এভাবেই চলবে)
এখন আমরা sin ও cos এর মান থেকে tan এর কোণের অনুপাতগুলো বের করব।
আমরা জানি,tan@=sin@/cos@
সুতরাং,tan0=sin0/cos0
…………….. =0/1=0
tan30=sin30/cos30 =(1/2)/( √3/2) =1/ √3
(এভাবে সহজেই tan এর অনুপাতগুলো বের করলাম)
এরপর cot@ =1/tan@ ব্যবহার করে সহজেই cot এর কোণের অনুপাতগুলোও বের করা যায়।
দেখলেন তো কত্ত সহজেই নিজ নিজ হাত ব্যবহার করেই ত্রিকোণমিতিক
অনুপাতগুলো বের করা সম্ভব।
এখন তো আর ত্রিকোনমিতিক অনুপাতগুলো মুখস্থ করার দরকার নায়।
গণিত এমনই এক জিনিস যাকে বাস্তবতার সাথে কল্পনা করতে পারলে খুব সহজেই সমস্যার সমাধান করা যায়।তাই নিজের চিন্তা-চেতনাকে অবশ্যই বৃদ্ধি করুন।





